Preethi Rajagopal's
Sunday, May 11, 2025
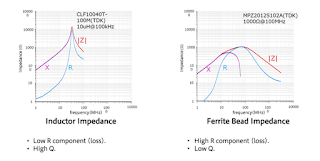
Difference between Inductor and ferrite bead
The direct current characteristics are also different. Inductors generally can tolerate comparatively large DC superposition currents, and within this range the DC current does not have much of an effect on the impedance, with almost no change in the resonance point. In contrast, ferrite beads easily reach saturation due to a DC current, and saturation causes the inductance to fall and the resonance point to shift to higher frequencies. Consequently the filter characteristics change, and so due caution is necessary Key differences:
Frequency Response:
Inductors have a more generally consistent impedance across a broader frequency range, while ferrite beads' impedance rises sharply at high frequencies.
Loss Characteristics:
Inductors typically have a lower loss factor (Q) than ferrite beads. Ferrite beads are designed to be more lossy at high frequencies to absorb and dissipate noise energy as heat.
Applications:
Inductors are used for a wider range of applications, including energy storage and general filtering. Ferrite beads are more specifically tailored for noise suppression and EMI filtering at high frequencies.
Construction:
Inductors are typically wound coils of wire, while ferrite beads are often small ferrite cylinders or toroids slipped over a wire
Ferrite Beads
Filtering high frequency power supply noise and cleanly sharing similar voltage supply rails (that is, analog and digital rails for mixed-signal ICs) while preserving high frequency isolation between the shared rails is the use of ferrite beads
A ferrite bead is a passive device that filters high frequency noise energy over a broad frequency range
It becomes resistive over its intended frequency range and dissipates the noise energy in the form of heat
The ferrite bead is connected in series with the power supply rail and is often combined with capacitors to ground on either side of the bead. This forms a low-pass filter network, further reducing the high frequency power supply noise.
However, improper use of ferrite beads in system design can lead to some detrimental issues. Some examples are unwanted resonance due to combining the bead with a decoupling capacitor for low-pass filtering and the effect of dc bias current dependency that degrades the EMI suppression capability of the bead. With proper understanding and consideration of the ferrite bead's behavior, these issues can be avoided.
Imagine you have a device, like a radio, and you want to make sure it doesn't pick up unwanted signals or noise. To do this, you use special components called beads and capacitors. These components help filter out the noise, kind of like how sunglasses filter out bright sunlight.
1. Unwanted Resonance: Sometimes, when you combine a bead with a capacitor to filter out noise, they can accidentally create a situation where certain unwanted signals get amplified instead of reduced. It's like if your sunglasses accidentally made some bright lights even brighter. This happens because the bead and capacitor can interact in a way that causes them to resonate, or vibrate, at certain frequencies, which can make the noise worse instead of better.
2. DC Bias Current Dependency: Beads are designed to suppress electromagnetic interference (EMI), which is unwanted noise that can affect electronic devices. However, beads can be sensitive to the amount of direct current (DC) flowing through them. If there's too much DC current, it can change how well the bead works, making it less effective at blocking noise. It's like if your sunglasses worked well in normal light but didn't work as well if the sun was too bright.
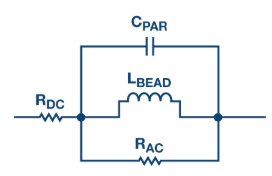
In summary, when using beads and capacitors to filter out noise, you have to be careful about how they interact and how much current is flowing through them, or else they might not work as intended. The important considerations that system designers need to be aware of when using ferrite beads in power supply systems such as impedance vs. frequency characteristics with varying dc bias current and unwanted LC resonance effects. Ultimately, to address the issue on the unwanted resonance, damping techniques will be introduced and a comparison of the effectiveness of each damping method will be presented. RDC corresponds to the dc resistance of the bead. CPAR, LBEAD, and RAC are (respectively) the parasitic capacitance, the bead inductance, and the ac resistance (ac core losses) associated with the bead. Ferrite beads are categorized by three response regions: inductive, resistive, and capacitive. These regions can be determined by looking at a ZRX plot where Z is the impedance, R is the resistance, and X is the reactance of the bead. To reduce high frequency noise, the bead must be in the resistive region; this is especially desirable for electromagnetic interference (EMI) filtering applications.The component acts like a resistor, which impedes the high frequency noise and dissipates it as heat. The resistive region occurs after the bead crossover frequency (X = R) and up to the point where the bead becomes capacitive. This capacitive point occurs at the frequency where the absolute value of capacitive reactance (–X) is equivalent to R. Let us take one example ferrite bead with above frequency characteristics. For the region on the measured ZRX plot where the bead appears most inductive (Z ≈ XL; LBEAD), the bead inductance is calculated by the following equation: where: f is the frequency point anywhere in the region the bead appears inductive. In this example, f = 30.7 MHz. XL is the reactance at 30.7 MHz, which is 233 Ω. above Equation yields an inductance value (LBEAD) of 1.208 µH. For the region where the bead appears most capacitive (Z ≈ |XC|; CPAR), the parasitic capacitance is calculated by the following equation: where: f is the frequency point anywhere in the region the bead appears capacitive. In this example, f = 803 MHz |XC| is the reactance at 803 MHz, which is 118.1 Ω. Above Equation yields a parasitic capacitance value (CPAR) of 1.678 pF. The dc resistance (RDC), which is 300 mΩ, is acquired from the manufacturer's data sheet. The ac resistance (RAC) is the peak impedance where the bead appears to be purely resistive. Calculate RAC by subtracting RDC from Z. Because RDC is very small compared to the peak impedance, it can be neglected. Therefore, in this case RAC is 1.082 kΩ. The ADIsimPE circuit simulator tool powered by SIMetrix/SIMPLIS was used to generate the impedance vs. the frequency response. Figure 2a shows the circuit simulation model with the calculated values and Figure below shows both the actual measurement and simulated result. In this example, the impedance curve from the circuit simulation model closely matches the measured one.
The ferrite bead model can be useful in noise filtering circuit design and analysis. For example, approximating the inductance of the bead can be helpful in determining the resonant frequency cutoff when combined with a decoupling capacitor in a low-pass filter network.
DC Bias Current Considerations
Selecting the right ferrite bead for power applications requires careful consideration not only of the filter bandwidth, but also of the impedance characteristics of the bead with respect to dc bias current. In most cases, manufacturers only specify the impedance of the bead at 100 MHz and publish data sheets with frequency response curves at zero dc bias current. However, when using ferrite beads for power supply filtering, the load current going through the ferrite bead is never zero, and as dc bias current increases from zero, all of these parameters change significantly
As the dc bias current increases, the core material begins to saturate, which significantly reduces the inductance of the ferrite bead. The degree of inductance saturation differs depending on the material used for the core of the component.
Figure below shows the typical dc bias dependency of the inductance for two ferrite beads. With 50% of the rated currents, the inductance decreases by up to 90%.
For effective power supply noise filtering, a design guideline is to use ferrite beads at about 20% of their rated dc current. As shown in these two examples, the inductance at 20% of the rated current drops to about 30% for the 6 A bead and to about 15% for the 3 A bead. The current rating of ferrite beads is an indication of the maximum current the device can take for a specified temperature rise and it is not a real operating point for filtering purposes.
In addition, the effect of dc bias current can be observed in the reduction of impedance values over frequency, which in turn reduces the effectiveness of the ferrite bead and its ability to remove EMI. Figures show how the impedance of the ferrite bead varies with dc bias current. By applying just 50% of the rated current, the effective impedance at 100 MHz dramatically drops from 100 Ω to 10 Ω for the TDK MPZ1608S101A (100 Ω, 3 A, 0603) and from 70 Ω to 15 Ω for the Würth Elektronik 742 792 510 (70 Ω, 6 A, 1812).
LC Resonance Effect
Resonance peaking is possible when implementing a ferrite bead together with a decoupling capacitor. This commonly overlooked effect can be detrimental because it may amplify ripple and noise in a given system instead of attenuating it. In many cases, this peaking occurs around the popular switching frequencies of dc-to-dc converters.
Peaking occurs when the resonant frequency of a low-pass filter network, formed by the ferrite bead inductance and the high Q decoupling capacitance, is below the crossover frequency of the bead. The resulting filter is underdamped. Figure 4a shows the measured impedance vs. frequency plot of the TDK MPZ1608S101A. The resistive component, which is depended upon to dissipate unwanted energy, does not become significant until reaching about the 20 MHz to 30 MHz range. Below this frequency, the ferrite bead still has a very high Q and acts like an ideal inductor. LC resonant frequencies for typical bead filters are generally in the 0.1 MHz to 10 MHz range. For typical switching frequencies in the 300 kHz to 5 MHz range, additional damping is required to reduce the filter Q.
Figure above shows the S21 frequency response of the bead and capacitor low-pass filter, which displays a peaking effect. The ferrite bead used is a TDK MPZ1608S101A (100 Ω, 3 A, 0603) and the decoupling capacitor used is a Murata GRM188R71H103KA01 low ESR ceramic capacitor (10 nF, X7R, 0603). Load current is in the microampere range.
An undamped ferrite bead filter can exhibit peaks from approximately 10 dB to approximately 15 dB depending on the Q of the filter circuit. In Figure, peaking occurs at around 2.5 MHz with as much as 10 dB gain.
In addition, signal gain can be seen from 1 MHz to 3.5 MHz. This peaking is problematic if it occurs in the frequency band in which the switching regulator operates. This amplifies the unwanted switching artifacts, which can wreak havoc on the performance of sensitive loads such as the phase-lock loop (PLL), voltage-controlled oscillators (VCOs), and high resolution analog-to-digital converters (ADCs). The result shown in Figure 4b has been taken with a very light load (in the microampere range), but this is a realistic application in sections of circuits that need just a few microamperes to 1 mA of load current or sections that are turned off to save power in some operating modes. This potential peaking creates additional noise in the system that can create unwanted crosstalk.
As an example, Figure below shows an ADP5071 application circuit with an implemented bead filter and Figure 6 shows the spectral plot at the positive output. The switching frequency is set at 2.4 MHz, the input voltage is 9 V, the output voltage is set at 16 V, and the load current of 5 mA
Resonant peaking occurs at around 2.5 MHz due to the inductance of the bead and the 10 nF ceramic capacitor. Instead of attenuating the fundamental ripple frequency at 2.4 MHz, a gain of 10 dB occurs.
Other factors that have an effect on the resonant peaks are the series and load impedances of the ferrite bead filter. Peaking is significantly reduced and damped for higher source resistance. However, the load regulation degrades with this approach, making it unrealistic in practice. The output voltage droops with load current due to the drop from the series resistance. Load impedance also affects the peaking response. Peaking is worse for light load conditions.
Damping Methods
Method A consists of adding a series resistor to the decoupling capacitor path that dampens the resonance of the system but degrades the bypass effectiveness at high frequencies. Method B consists of adding a small parallel resistor across the ferrite bead that also dampens the resonance of the system. However, the attenuation characteristic of the filter is reduced at high frequencies. Figure 8 show the impedance vs. frequency curve of the MPZ1608S101A with and without a 10 Ω parallel resistor. The light green dashed curve is the overall impedance of the bead with a 10 Ω resistor in parallel. The impedance of the bead and resistor combination is significantly reduced and is dominated by the 10 Ω resistor. However, the 3.8 MHz crossover frequency for the bead with the 10 Ω parallel resistor is much lower than the crossover frequency of the bead on its own at 40.3 MHz. The bead appears resistive at a much lower frequency range, lowering the Q for improved damped performance. Method C consists of adding a large capacitor (CDAMP) with a series damping resistor (RDAMP), which is often an optimal solution.
Adding the capacitor and resistor damps the resonance of the system and does not degrade the bypass effectiveness at high frequencies. Implementing this method avoids excessive power dissipation on the resistor due to a large dc blocking capacitor. The capacitor must be much larger than the sum of all decoupling capacitors, which reduces the required damping resistor value. The capacitor impedance must be sufficiently smaller than the damping resistance at the resonant frequency to reduce the peaking.
Figure below shows the ADP5071 positive output spectral plot with Method C damping implemented on the application circuit shown in Figure. The CDAMP and RDAMP used are a 1 µF ceramic capacitor and a 2 Ω SMD resistor, respectively. The fundamental ripple at 2.4 MHz is reduced by 5 dB as opposed to the 10 dB gain shown in Figure. Generally, Method C is the most elegant and is implemented by adding a resistor in series with a ceramic capacitor rather than buying an expensive dedicated damping capacitor. The safest designs always include a resistor that can be tweaked during prototyping and that can be eliminated if not necessary. The only drawbacks are the additional component cost and greater required board space.
Conclusion:
A dc bias current greater than 20% of the rated current can cause a significant drop in the bead inductance
Such a current can also reduce the effective impedance of the bead and degrade its EMI filtering capability.
When using ferrite beads in supply rail with dc bias current, ensure that the current does not cause saturation of the ferrite material and produce significant change of inductance.
Because the ferrite bead is inductive, do not use it with high Q decoupling capacitors without careful attention. Doing so can do more harm than good by producing unwanted resonance in a circuit. However, the damping methods proposed in this article offer an easy solution by using a large decoupling capacitor in series with a damping resistor across the load, thus avoiding unwanted resonance. Applying ferrite beads correctly can be an effective and inexpensive way to reduce high frequency noise and switching transients
Saturday, May 10, 2025
My Journey in stepping up my career
Hi,
I am a Hardware Engineer who designs board. The role is, with product requirement (speed, spec, budget, power, back-up, mechanical, standards to pass, etc., ) I start with high level architecture, choosing components, block diagram, etc. Once on getting collective decision to proceed, we proceed with schematics, and with some level of maturity we procced with layout feasibility, mechanical feasibility etc.,
We also do DC analysis (Noise margin), AC analysis (Setup time, hold time, etc.,) Logic level analysis (requirement of level translator), Power budget analysis, Thermal analysis etc., in schematic phase
Once on moving into layout phase, we evaluate the stackup, x, y dimension, routing of high speed signals, then low speed signals, Power shapes etc.,
With completion, we proceed with SI and PI analysis.
Parallelly, Mechanical check with Dxf, thermal simulaiton with max powers are done.
Debugging happens if any of these analysis fail.
Since practically sticking to all the guidelines is not possible , we proceed with some low level of risk provided , we it fine to allow that risk.
once on completion of all these, we proceed with tapeout (Gerber release to Fab house). There will be a week + time for building the boards. Meanwhile we will prepare for bring up and validation with proper plan document.
From Fab house, the boards goes to Assembly house, where the components are assembled and soldered on the board.
Post that , bring up and validation of each and every interface / power section involved in the board.
Followed by detailed report preparation, scompliance testing (FCC, UL etc.,) , thermal tolerance test (operating temperture with Thermal chambers).
Above is a brief what I do.
I initially started my career in a startup environment - where it is all too fast paced, leading to fast learning. But there is a drawback, frequently switching from one domain to other like from power electronics to high speed, high speed to analog, etc., Also, I didnt have full exposure with Compliance testing or thermal chamber. Because, I am a female employee and our company didnt have any inhouse compliance testing lab / thermal chamber. So, one of the male employee in project goes to different city for compliance testing. I was just communicating with that employee, wherever it was failing, we were checking that and helping to fix that issue.
I tried so hard, but it was very difficult to switch to another company as they are asking questions so detailed in each and every interface and expectation was to have experience from the scratch to mass production.
Finally after having 5 years of experience, I switched to one of the best product based company.
And now it has been 4 years here. I feel a bit stagnant in pay as well as career. I want to switch to a different company with better role (Hardware Engineer / Post silicon validation) and pay scale, where I will deal with details , I should improvise and be contributing greatness to the industry.
So, I have a plan as listed below starting from today.
First I will focus on brushing up what I have worked on. Then I will focus on improving embedded SW as well.
Need to brush up on :
| S. No. | Topics to explore | Schedule |
| 1 | Ferrite Bead | May 11 |
| 2 | Inductor | May 11 |
| 3 | Resistor | May 11 |
| 4 | Capacitor | May 11 |
| 5 | Filter design | May 12 |
| 6 | MOSFET - Application | May 12 |
| 7 | Diode | May 12 |
| 8 | clipper | May 12 |
| 9 | clamper | May 12 |
| 10 | Opamp | May 13 |
| 11 | Reset | May 14 |
| 12 | watch dog timer | May 14 |
| 13 | switch debouncing | May 14 |
| 14 | FPGA | May 14 |
| 15 | ASIC | May 14 |
| 16 | DDR4 | May 15 |
| 17 | DDR5 | May 15 |
| 18 | LPDDR5 | May 16 |
| 19 | SODIMM5 | May 16 |
| 20 | LPCAMM | May 16 |
| 21 | Power sequencing | May 17 |
| 22 | LDO | May 17 |
| 23 | Boost | May 17 |
| 24 | Buck | May 17 |
| 25 | Buck boost | May 17 |
| 26 | Batteries (Li - IOn, LFP) | May 18 |
| 27 | Fuel gauge | May 18 |
| 28 | Battery charger | May 18 |
| 29 | Battery protection | May 18 |
| 30 | Straps | May 19 |
| 31 | Multimeter | May 19 |
| 32 | Edge rate | May 19 |
| 33 | Surge | May 19 |
| 34 | EFT | May 19 |
| 35 | ESD | May 19 |
| 36 | Termination | May 19 |
| 37 | I2C | May 20 |
| 38 | I3C | May 20 |
| 39 | UART | May 21 |
| 40 | SPI | May 21 |
| 41 | RS232 | May 22 |
| 42 | RS485 | May 22 |
| 43 | USB 2 | May 23 |
| 44 | USB 3 | May 23 |
| 45 | TBT | May 24 |
| 46 | RGMII | May 25 |
| 47 | SGMII | May 25 |
| 48 | Ethernet | May 25 |
| 49 | SFP | May 26 |
| 50 | SFP+ | May 26 |
| 51 | POE - PD | May 26 |
| 52 | LED Display | May 27 |
| 53 | LCD Display | May 27 |
| 54 | LVDS | May 27 |
| 55 | RGB | May 27 |
| 56 | PCIe | May 28 |
| 57 | SSD | May 28 |
| 58 | SATA | May 28 |
| 59 | NAND Flash | May 28 |
| 60 | NOR Flash | May 28 |
| 61 | I2S | May 29 |
| 62 | Soundwire | May 29 |
| 63 | HDA | May 29 |
| 64 | Audio Codec | May 30 |
| 65 | Audio Amplifier | May 30 |
| 66 | Audio - Mic | May 30 |
| 67 | Audio - Speaker | May 30 |
| 68 | Audio - Headphone | May 30 |
| 69 | Audio Validation | May 31 |
| 70 | Audio Precision system | May 31 |
| 71 | Audio Drivers | May 31 |
| 72 | Boot scheme in Laptop | June 1 |
| 73 | Server | June 1 |
| 74 | 5G Small Cell Indoor DU | June 1 |
| 75 | Marvel CN9130 processor for L2/L3 processing | June 1 |
| 76 | XILINX XCZU21DR (RFSOC) baseband processor +FPGA for L1 processing. | June 1 |
| 77 | High speed Interface | June 2 |
| 78 | PCB Stackup, Layer, spacing | June 2 |
| 79 | Grounding, PCB layout guidelines | June 2 |
| 80 | stripline, Microstripline | June 3 |
| 81 | via, crosstalk, Noise margin | June 3 |
| 82 | AC Analysis | June 3 |
| 83 | SI | June 4 |
| 84 | Antenna Tuning | June 5 |
| 85 | Network Analyser | June 5 |
| 86 | Jitter, eye diagram | June 6 |
| 87 | Vector Analyser | June 7 |
| 88 | BERT | June 8 |
| 89 | IMVP, SVID | June 9 |
| 90 | Processor state, RPMC | June 10 |
| 91 | PI | June 10 |
Need to learn Embedded SW: